Got your eye on a flashy new car?
Or perhaps you’re considering a new home?
If you don’t have the cash to pay for either of these, you’ll need to get a loan.
And before you jump in head-first, you’ll want to know how much you’ll be paying each month, and perhaps you’ll want to know
the obscene amount of how much interest you’ll end up paying over the life of the loan.
Sure, there are truckloads of loan calculators out there on the web… They’re a dime a dozen.
But who needs those when you have the raw power of SQL Server at your fingertips?
This blog entry will demonstrate how to create a loan payment schedule based on a fixed interest rate with compounded interest, and, as always, we’ll go a little bit beyond that to explore some other things.
The monthly payment amount,
c, is expressed by the following formula:
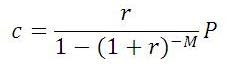
where
P is the loan amount,
M is the number of months of the loan, and
r is the monthly interest rate expressed as a decimal.
The balance of the loan after payment number
N is expressed by the following formula:
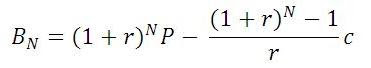
With all this in mind, here is a stored procedure to produce a payment schedule:
use tempdb;
go
if object_id('usp_LoanSchedule') is not null drop procedure usp_LoanSchedule;
go
create procedure usp_LoanSchedule
@LoanAmount numeric(10,2)
,@AnnualRate numeric(10,8) /* Expressed as percent */
,@NumberOfMonths int
,@StartDate datetime
as
with InputVariables as
(
select P,M,R
,C=round((P*R)/(1-power(1+R,-M)),2)
from (select P=@LoanAmount
,M=@NumberOfMonths
,R=@AnnualRate/12/100) InputData
)
,MonthlyPayments(PmtNo
,PmtDate
,Balance
,Principle
,Interest
,CumulPrinciple
,CumulInterest) as
(
select N
,dateadd(month,datediff(month,'19000101',@StartDate),'19000101')
,cast(NewBalance as numeric(10,2))
,cast(P-NewBalance as numeric(10,2))
,cast(C-(P-NewBalance) as numeric(10,2))
,cast(P-NewBalance as numeric(10,2))
,cast(C-(P-NewBalance) as numeric(10,2))
from InputVariables
cross apply (select N=1) CalcPmtNo
cross apply (select NewBalance=round(P*power(1+R,N)
-(power(1+R,N)-1)*C/R,2)) CalcNewBalance
union all
select N
,dateadd(month,1,mp.PmtDate)
,cast(NewBalance as numeric(10,2))
,cast(mp.Balance-NewBalance as numeric(10,2))
,cast(C-(mp.Balance-NewBalance) as numeric(10,2))
,cast(mp.CumulPrinciple+mp.Balance-NewBalance as numeric(10,2))
,cast(mp.CumulInterest+C-(mp.Balance-NewBalance) as numeric(10,2))
from MonthlyPayments mp
cross join InputVariables
cross apply (select N=mp.PmtNo+1) CalcPmtNo
cross apply (select NewBalance=case
when N=M
then 0.00 /* Last Payment */
else round(P*power(1+R,N)
-(power(1+R,N)-1)*C/R,2)
end) CalcNewBalance
where N<=M
)
select PmtNo
,PmtMonth=datename(month,PmtDate)+str(year(PmtDate),5)
,PmtAmount=Principle+Interest
,Principle
,Interest
,CumulPrinciple
,CumulInterest
,Balance
from MonthlyPayments
order by PmtNo
option (maxrecursion 1000)
;
If we want to buy a $20,000 car at 6.8% (annual) interest with a 5-year term (60 months) with our first payment in December 2009, then we can call it like so:
exec usp_LoanSchedule @LoanAmount = 20000
,@AnnualRate = 6.8
,@NumberOfMonths = 60
,@StartDate = '20091201'
/*
PmtNo PmtMonth PmtAmount Principle Interest CumulPrinciple CumulInterest Balance
----- -------------- --------- --------- -------- -------------- ------------- --------
1 December 2009 394.14 280.81 113.33 280.81 113.33 19719.19
2 January 2010 394.14 282.39 111.75 563.20 225.08 19436.80
3 February 2010 394.14 284.00 110.14 847.20 335.22 19152.80
4 March 2010 394.14 285.61 108.53 1132.81 443.75 18867.19
... ... ... ... ... ... ... ...
57 August 2014 394.14 385.33 8.81 18830.89 3635.09 1169.11
58 September 2014 394.14 387.52 6.62 19218.41 3641.71 781.59
59 October 2014 394.14 389.71 4.43 19608.12 3646.14 391.88
60 November 2014 394.14 391.88 2.26 20000.00 3648.40 0.00
*/
Let’s go over how the logic works.
The procedure essentially consists of a single SELECT statement, which is made up of two CTE’s (Common Table Expressions).
The first CTE is called InputVariables, and it just produces a small one-row table of the variables that we need for the calculations… in other words, our friends
P,
M,
r, and
c. Note how
r is calculated by dividing the @AnnualRate parameter by 12 (to get a monthly rate) and then by 100 (to represent the rate as a decimal). Also note how
c (the monthly payment amount) was calculated based on the other 3 variables.
I could have just created local variables (@P, @M, @R, and @C) instead of setting them up in a CTE, but I had two reasons for not doing that. First of all, I didn’t want all those pesky at-signs (@) to be all throughout the code and second, I wanted to encapsulate the entire creation of the loan schedule table in a single SELECT statement (I’ll explain why later).
The second CTE, called MonthlyPayments, is a recursive one. The first part of the recursive CTE (before the UNION ALL) is the anchor. It produces the data for the very first payment (note how I also adjust the first payment date to the first of the month). The second part (the recursive part) of the CTE builds upon that, creating the second payment, then the third, and so on, up until the last payment. It will continue tacking on payments as long as its WHERE clause (WHERE N<=M) is true… in other words, as long as the Payment Number (N) is less than or equal to the number of months of the loan (M). Once the WHERE clause evaluates to false (when N>M), then it will stop.
Both the anchor and the recursive part of the CTE use a couple of CROSS APPLYs. The first CROSS APPLY establishes a new column N, the Payment Number. The only reason I do this is because I want to use N in the calculation of the Balance. You’ll recall that the formula for the Balance uses N as one of its variables.
The second CROSS APPLY is the calculation of that NewBalance, making use of
P,
r,
N, and
c. Note the CASE statement that checks if we are processing the final payment (CASE WHEN N=M) and, if so, it forces the final balance to be zero.
The Principle of the payment is calculated by subtracting the NewBalance from the Balance of the previous payment (or in the case of the very first payment, by subtracting NewBalance from the original loan amount
P). The Interest part of the payment is calculated by simply subtracting the Principle from the Payment Amount (
c).
Since the recursive CTE is building the schedule one payment at a time, we can take advantage of that and calculate cumulative totals for the Principle and the Interest (CumulPrinciple and CumulInterest) as we go along.
Finally, the main SELECT statement pulls all the rows from the MonthlyPayments recursive CTE, dressing up the date by spelling out the month’s name and ORDERing BY the PmtNo.
Note the OPTION clause. By default, the maximum number of recursion levels is 100. The number of levels of recursion we will reach depends on the value of @NumberOfMonths that is passed to the procedure. If we’re doing a mortgage payment that spans 30 years, then @NumberOfMonths will be 360 and we will need a level of recursion of at least 360 or else we will get this message:
/*
Msg 530: The statement terminated.
The maximum recursion 100 has been exhausted before statement completion.
*/
So our general MAXRECURSION value of 1000 should certainly be reasonable enough, assuming that no loan is going to last more than 83 years.
Great! We have a stored procedure that produces a loan schedule! Terrific!
Now what?
Not much, that’s what. This stored procedure works just fine, but we can’t really
do anything with it. All we can do is EXECUTE it. Unless we INSERT its result set into a temporary table, we can’t query any important information out of it.
However, we
could query information out of this loan schedule data if we created an inline table-valued function (TVF) instead of the stored procedure, like so:
use tempdb;
go
if object_id('ufn_LoanSchedule') is not null drop function ufn_LoanSchedule;
go
create function ufn_LoanSchedule
(
@LoanAmount numeric(10,2)
,@AnnualRate numeric(10,8) /* Expressed as percent */
,@NumberOfMonths int
,@StartDate datetime
)
returns table
as
return
with InputVariables as
(
select P,M,R
,C=round((P*R)/(1-power(1+R,-M)),2)
from (select P=@LoanAmount
,M=@NumberOfMonths
,R=@AnnualRate/12/100) InputData
)
,MonthlyPayments(PmtNo
,PmtDate
,Balance
,Principle
,Interest
,CumulPrinciple
,CumulInterest) as
(
select N
,dateadd(month,datediff(month,'19000101',@StartDate),'19000101')
,cast(NewBalance as numeric(10,2))
,cast(P-NewBalance as numeric(10,2))
,cast(C-(P-NewBalance) as numeric(10,2))
,cast(P-NewBalance as numeric(10,2))
,cast(C-(P-NewBalance) as numeric(10,2))
from InputVariables
cross apply (select N=1) CalcPmtNo
cross apply (select NewBalance=round(P*power(1+R,N)
-(power(1+R,N)-1)*C/R,2)) CalcNewBalance
union all
select N
,dateadd(month,1,mp.PmtDate)
,cast(NewBalance as numeric(10,2))
,cast(mp.Balance-NewBalance as numeric(10,2))
,cast(C-(mp.Balance-NewBalance) as numeric(10,2))
,cast(mp.CumulPrinciple+mp.Balance-NewBalance as numeric(10,2))
,cast(mp.CumulInterest+C-(mp.Balance-NewBalance) as numeric(10,2))
from MonthlyPayments mp
cross join InputVariables
cross apply (select N=mp.PmtNo+1) CalcPmtNo
cross apply (select NewBalance=case
when N=M
then 0.00 /* Last Payment */
else round(P*power(1+R,N)
-(power(1+R,N)-1)*C/R,2)
end) CalcNewBalance
where N<=M
)
select PmtNo
,PmtDate
,PmtAmount=Principle+Interest
,Principle
,Interest
,CumulPrinciple
,CumulInterest
,Balance
from MonthlyPayments
;
(This is why I originally created a single one-stop-shopping query in our original stored procedure without the use of local variables… so that I could easily translate it into an in-line TVF).
Now we can call the TVF just as if it were a table, pulling out any columns we wish:
select PmtNo
,PmtDate
,Principle
,Interest
,Balance
from dbo.ufn_LoanSchedule(20000,6.8,60,'20091201')
order by PmtNo
/*
PmtNo PmtDate Principle Interest Balance
----- ----------------------- --------- -------- --------
1 2009-12-01 00:00:00.000 280.81 113.33 19719.19
2 2010-01-01 00:00:00.000 282.39 111.75 19436.80
3 2010-02-01 00:00:00.000 284.00 110.14 19152.80
4 2010-03-01 00:00:00.000 285.61 108.53 18867.19
... ... ... ... ...
57 2014-08-01 00:00:00.000 385.33 8.81 1169.11
58 2014-09-01 00:00:00.000 387.52 6.62 781.59
59 2014-10-01 00:00:00.000 389.71 4.43 391.88
60 2014-11-01 00:00:00.000 391.88 2.26 0.00
*/
Look back at the code where we created the TVF. Did you notice something missing in the definition? Two things, actually. I deliberately left out the ORDER BY clause because we may want to order the data in a different way when we call the TVF. But the OPTION clause is also missing that specifies the MAXRECURSION value. T-SQL will not allow it in a query that’s part of a TVF definition. If we were to tack it on to the end of the query and try to CREATE the FUNCTION, we’d get the following error message:
/*
Msg 156, Level 15, State 1, Procedure ufn_LoanSchedule, Line 67
Incorrect syntax near the keyword 'option'.
*/
Since we cannot specify any MAXRECURSION in the TVF definition, it is (unfortunately) up to us to include the OPTION clause in any query that calls the TVF if we know that we are going to breach the minimum level of 100.
So, for example, let’s say we have just bought a quaint little cottage for $500,000. (Don’t scoff… that price is dirt cheap for a humble little abode here in the San Francisco Bay Area). We get a 30-year (360-month) fixed loan with a 5% interest rate, with our first payment due in January 2010. We need to add the OPTION clause to the following query to prevent an error:
select PmtNo
,PmtDate
,Principle
,Interest
,Balance
from dbo.ufn_LoanSchedule(500000,5,360,'20100101')
option (maxrecursion 360)
/*
PmtNo PmtDate Principle Interest Balance
----- ----------------------- --------- -------- ---------
1 2010-01-01 00:00:00.000 600.78 2083.33 499399.22
2 2010-02-01 00:00:00.000 603.28 2080.83 498795.94
3 2010-03-01 00:00:00.000 605.79 2078.32 498190.15
4 2010-04-01 00:00:00.000 608.32 2075.79 497581.83
... ... ... ... ...
357 2039-09-01 00:00:00.000 2639.84 44.27 7984.14
358 2039-10-01 00:00:00.000 2650.84 33.27 5333.30
359 2039-11-01 00:00:00.000 2661.89 22.22 2671.41
360 2039-12-01 00:00:00.000 2671.41 12.70 0.00
*/
Anyway, now that we have a TVF, we can get some interesting information from the loan schedule data.
For example, using our mortgage scenario, how much can we write off in mortgage interest on our income taxes in the year 2012?:
select TotalInterest=sum(Interest)
from dbo.ufn_LoanSchedule(500000,5,360,'20100101')
where year(PmtDate)=2012
option (maxrecursion 360)
/*
TotalInterest
-------------
24058.33
*/
What will our loan balance be at the end of 2015?:
select Balance
from dbo.ufn_LoanSchedule(500000,5,360,'20100101')
where PmtDate='20151201'
order by PmtNo
option (maxrecursion 360)
/*
Balance
---------
449676.39
*/
How long will it take for us to pay off half of the loan?:
select top 1 PmtNo,PmtDate
from dbo.ufn_LoanSchedule(500000,5,360,'20100101')
where CumulPrinciple>=Balance
order by PmtNo
option (maxrecursion 360)
/*
PmtNo PmtDate
----- -----------------------
242 2030-02-01 00:00:00.000
*/
(Yikes… That’s the problem with how these loans work. It’ll take over 20 years of the 30-year loan term to pay off half of the principle.)
Finally, we can test out different rates and see how the monthly payment changes and how much total cumulative interest we’ll end up paying for each rate:
select Rate
,PmtAmount
,CumulInterest
from (select 5.1 union all
select 5.3 union all
select 5.5 union all
select 5.7 union all
select 5.9) Rates(Rate)
cross apply dbo.ufn_LoanSchedule(500000,Rate,360,'20100101')
where PmtNo=360
option (maxrecursion 360)
/*
Rate PmtAmount CumulInterest
---- --------- -------------
5.1 2714.75 477310.00
5.3 2776.52 499547.20
5.5 2838.95 522022.00
5.7 2902.00 544720.00
5.9 2965.68 567644.80
*/
(Don’t you find it
disgusting interesting how you pay more in interest over the life of the loan than you do in principle if your rate is a little over 5.3%?).
I hope this article has been helpful not just in showing how to calculate loan schedule data, but also in demonstrating recursive CTE’s and TVF’s and other techniques. I certainly learned something I didn’t expect (the inability to specify a MAXRECURSION value in a TVF) in putting the article together.
I’ll bet that your borrowing future will be brighter now that you have the tools to analyze potential loans. From now on, you’ll be able to make those payments with a smile on your face.
Yeah, right.
 I don't have any heavy in-depth T-SQL code or analysis today…
I don't have any heavy in-depth T-SQL code or analysis today…